Conformal Surface Splines
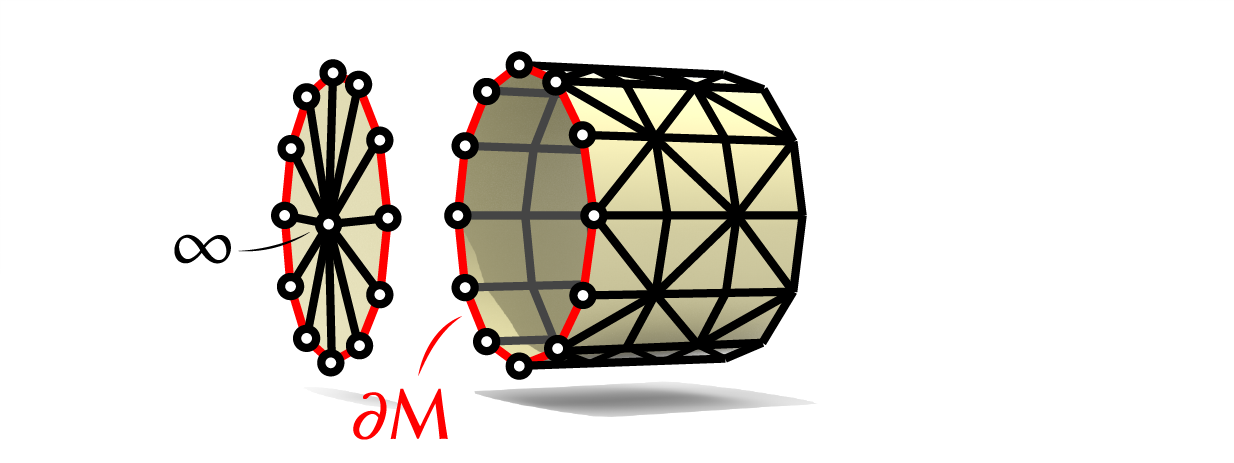
Restricting the admissible conformal variations to those which keep the metric on the boundary fixed up a gloabl scale results in free boundary conditions that are especially well-suited for surface modeling. In the discrete setting, this condition can be interpreted equivalently as fixing the conformal class on the surface filled in with a disk at infinity.
We introduce a family of boundary conditions and point constraints for conformal immersions that increase the controllability of surfaces defined as minimizers of conformal variational problems. Our free boundary conditions fix the metric on the boundary, up to a global scale, and admit a discretization compatible with discrete conformal equivalence. We also introduce constraints on the conformal scale factor, enforcing rigidity of the geometry in regions of interest, and describe how in the presence of point constraints the conformal class encodes knot points of the spline that can be directly manipulated. To control the tangent planes, we introduce flux constraints balancing the internal material stresses. The collection of these point constraints provide intuitive controls for exploring a subspace of conformal immersions interpolating a fixed set of points in space. We demonstrate the applicability of our framework to geometric modeling, mathematical visualization, and form finding.